Neural networks for regression - a comprehensive overview - Part 6
After examining how neural networks can effectively approximate non-linear functions, we will now turn our attention to their weaknesses.
How many hidden units should we use ?
In the previous examples, we arbitrarily used ten hidden units for our neural network. But is this a suitable value ? To determine that, we will experiment with different values and see whether the function is still accurately approximated.
We will use the function $x \mapsto cos 6x$ for our experiments.
With 2 hidden units
We will begin our experiment by using only two hidden units to see how the neural network behaves.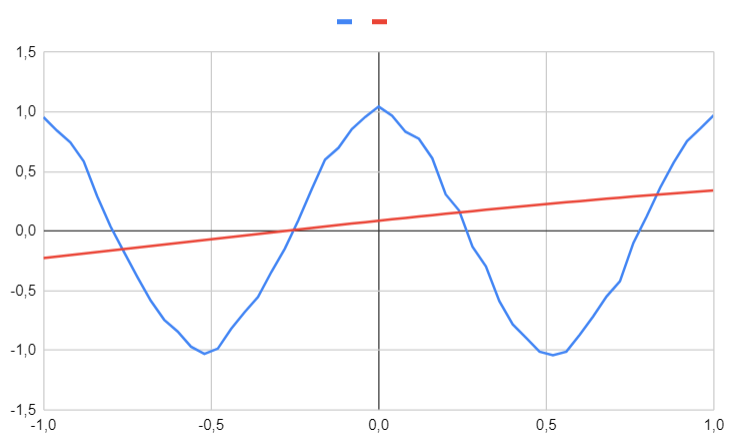
It is clear that the approximation is quite poor, indicating that the network lacks sufficient flexibility to accurately model the function. This phenomenon is referred to as underfitting.
With 4 hidden units
We will conduct the same experiment, but this time with four hidden units.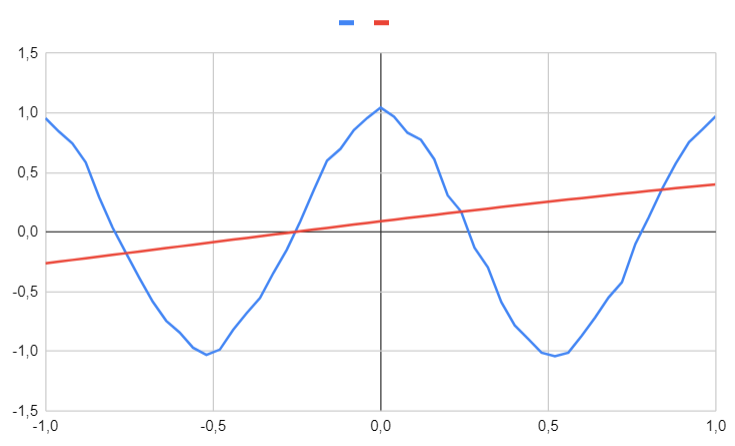
It is clear that the approximation is still quite poor.
With 6 hidden units
We will conduct the same experiment, but this time with six hidden units.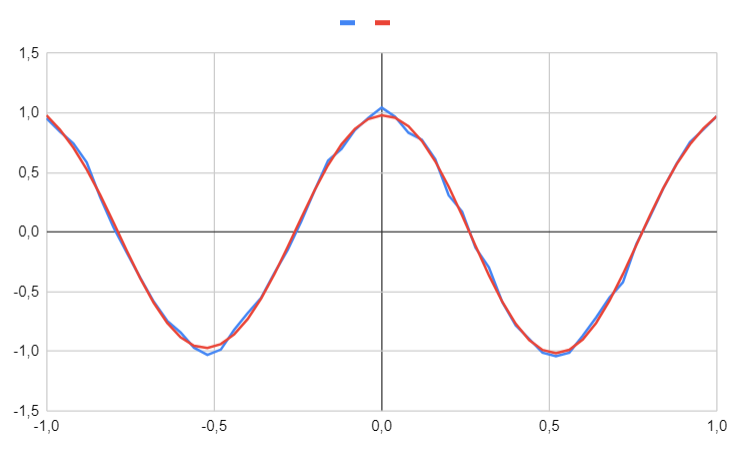
The approximation is now very accurate; however, this example illustrates that it can be quite challenging to determine the optimal number of hidden units. In our case, it was relatively easy to determine if the approximation was good; however, in real-world scenarios with hundreds or thousands of dimensions, this becomes much more complicated. Identifying the optimal number of hidden units is more of an art than a science.
If there are not enough hidden units, there is a risk of encountering the underfitting phenomenon. Conversely, if there are too many hidden units, we may face overfitting or consume excessive resources.
Can a neural network extrapolate values ?
In the previous post, we examined how a neural network can interpolate unseen values. We specifically looked at the value $0.753$ and found that it yields a relatively accurate prediction. However, we can question whether a neural network can determine an extrapolated value (specifically, a value outside the initial interval). In our case, what would be the predicted value for $2$ for example ?
Once again, we will use the function $x \mapsto cos 6x$ for our experiments and set the number of hidden units to 6.
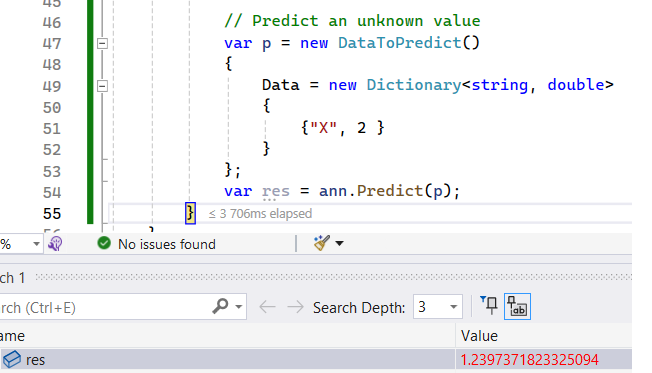
The neural network predicts $1.2397$, while the expected value is $0.8438$.
As a result, a neural network is unable to accurately predict extrapolated values. This phenomenon has significant implications: to ensure accurate predictions for all our inputs, we must ensure the completeness of our dataset. Specifically, it is essential to have representative values for all possible features. Otherwise, the network may produce unreliable predictions.
Now that we have explored neural networks for regression in depth on toy examples, we will examine how they can be applied in a real-world scenario.
Neural networks for regression - a comprehensive overview - Part 7