Neural networks for regression - a comprehensive overview - Part 5
After all this effort, we will reap the rewards of our labor by demonstrating how a neural network can effectively model different functions.
$x \mapsto x^2$
Our goal is to verify that a neural network can approximate the function $x \mapsto x^2$.
Defining the dataset
Our dataset consists of one input and one output, specifically modeling the function $x \mapsto x^2$. Data points are uniformly sampled for $x$ over the interval $[-1, 1]$, and the corresponding values have been subjected to noise.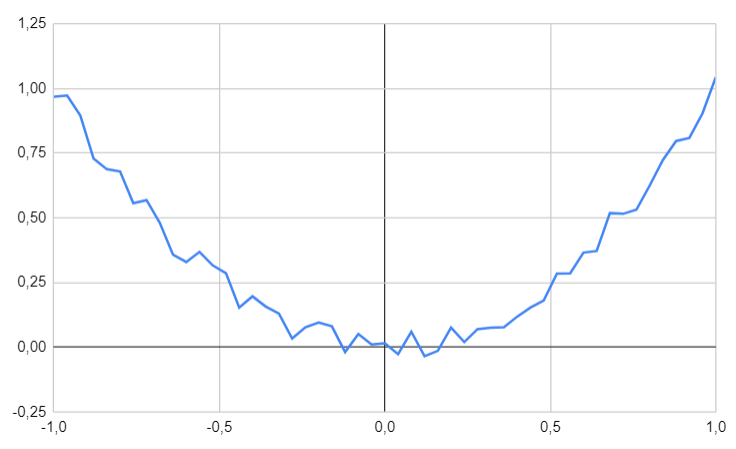
Our objective is to predict values for inputs that have not been seen before.
Training the neural network
We will start by using a neural network with ten hidden layers.
1internal class Program
2{
3 static void Main(string[] args)
4 {
5 var path = AppContext.BaseDirectory + "/dataset01.csv";
6 var dataset = DataSet.Load(path); var numberOfFeatures = dataset.Features.Count;
7
8 var hiddenActivation = new TanhActivationFunction();
9 var trainer = new GradientDescentANNTrainer();
10
11 // Define the neural network
12 var ann = new ANNForRegression(numberOfFeatures, 10, hiddenActivation, trainer);
13
14 // Train the network with the dataset
15 ann.Train(dataset);
16
17 // Predict an unknown value
18 var p = new DataToPredict()
19 {
20 Data = new Dictionary<string, double>
21 {
22 {"X", 0.753 }
23 }
24 };
25 var res = ann.Predict(p);
26 }
27}
Here is what the neural network determines for the labeled values.
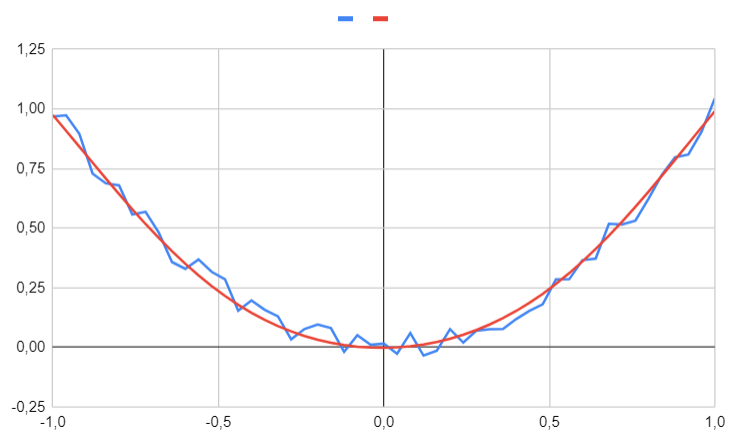
We can see that the neural network successfully identifies the underlying function. Now, let's predict an unseen value, such as $0.753$.
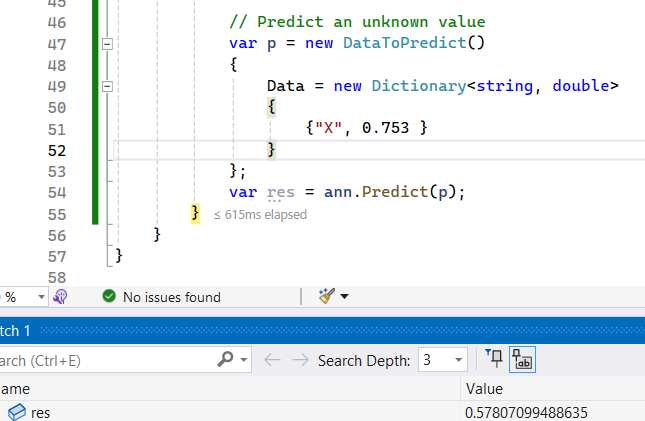
The neural network predicts $0.5781$, while the expected value is $0.5670$.
$x \mapsto cos6x$
Our goal is to verify that a neural network can approximate the function $x \mapsto cos6x$.
Defining the dataset
Our dataset consists of one input and one output, specifically modeling the function $x \mapsto cos6x$. Data points are uniformly sampled for $x$ over the interval $[-1, 1]$, and the corresponding values have been subjected to noise.
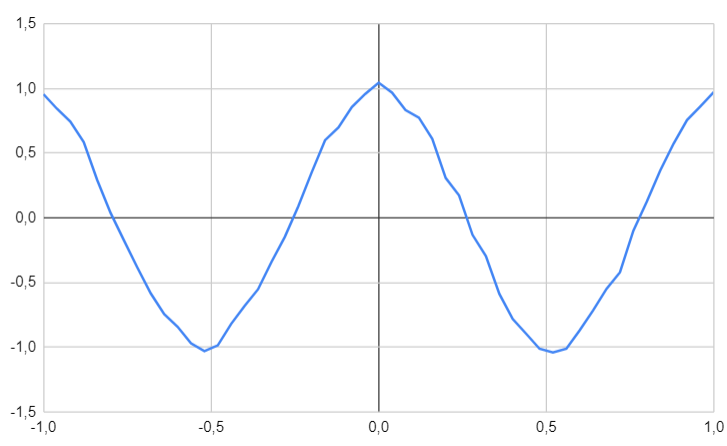
Our objective is to predict values for inputs that have not been seen before.
Training the neural network
We will start by using a neural network with ten hidden layers.
1internal class Program
2{
3 static void Main(string[] args)
4 {
5 var path = AppContext.BaseDirectory + "/dataset02.csv";
6 var dataset = DataSet.Load(path); var numberOfFeatures = dataset.Features.Count;
7
8 var hiddenActivation = new TanhActivationFunction();
9 var trainer = new GradientDescentANNTrainer();
10
11 // Define the neural network
12 var ann = new ANNForRegression(numberOfFeatures, 10, hiddenActivation, trainer);
13
14 // Train the network with the dataset
15 ann.Train(dataset);
16
17 // Predict an unknown value
18 var p = new DataToPredict()
19 {
20 Data = new Dictionary<string, double>
21 {
22 {"X", 0.753 }
23 }
24 };
25 var res = ann.Predict(p);
26 }
27}
Here is what the neural network determines for the labeled values.
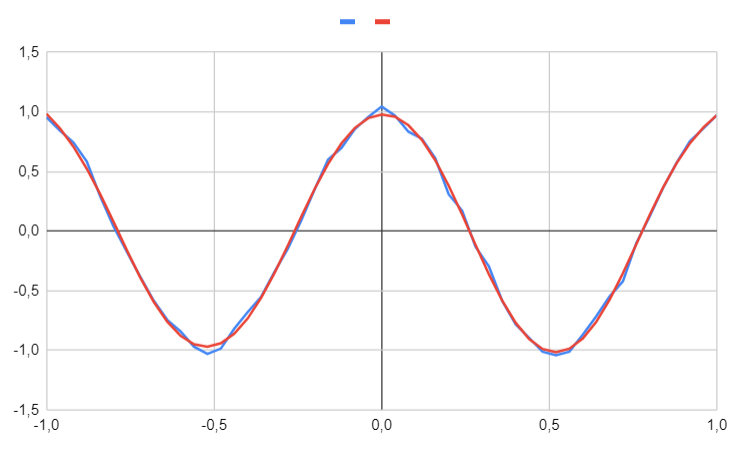
We can see that the neural network successfully identifies the underlying function. Now, let's predict an unseen value, such as $0.753$.
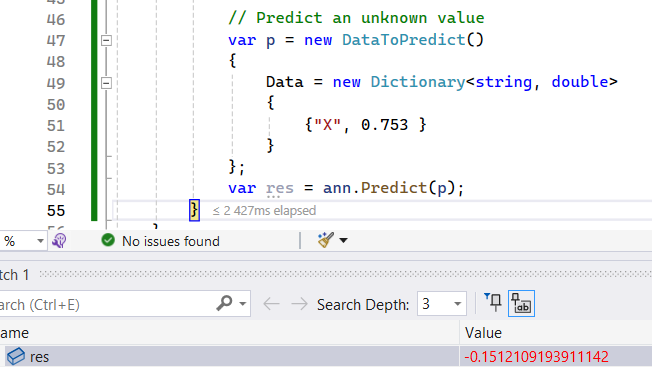
The neural network predicts $-0.1512$, while the expected value is $-0.1932$.
$x \mapsto H(x)$
Our goal is to verify that a neural network can approximate the Heaviside function.
Defining the dataset
Our dataset consists of one input and one output, specifically modeling the Heaviside function. Data points are uniformly sampled for $x$ over the interval $[-1, 1]$, and the corresponding values have been subjected to noise.
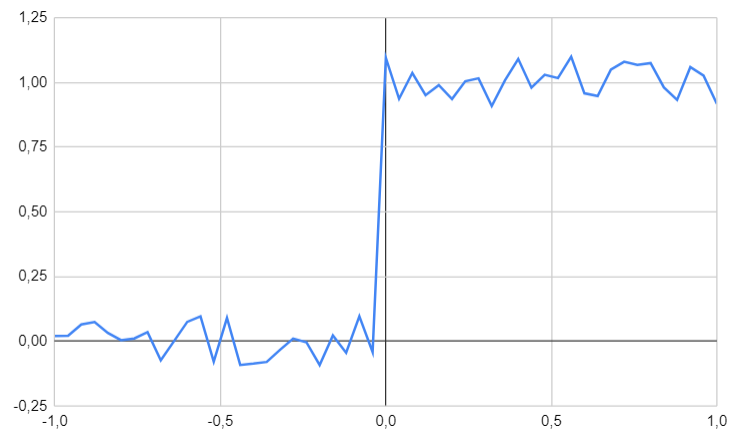
Our objective is to predict values for inputs that have not been seen before.
Training the neural network
We will start by using a neural network with ten hidden layers.
1internal class Program
2{
3 static void Main(string[] args)
4 {
5 var path = AppContext.BaseDirectory + "/dataset04.csv";
6 var dataset = DataSet.Load(path); var numberOfFeatures = dataset.Features.Count;
7
8 var hiddenActivation = new TanhActivationFunction();
9 var trainer = new GradientDescentANNTrainer();
10
11 // Define the neural network
12 var ann = new ANNForRegression(numberOfFeatures, 10, hiddenActivation, trainer);
13
14 // Train the network with the dataset
15 ann.Train(dataset);
16
17 // Predict an unknown value
18 var p = new DataToPredict()
19 {
20 Data = new Dictionary<string, double>
21 {
22 {"X", 0.753 }
23 }
24 };
25 var res = ann.Predict(p);
26 }
27}
Here is what the neural network determines for the labeled values.
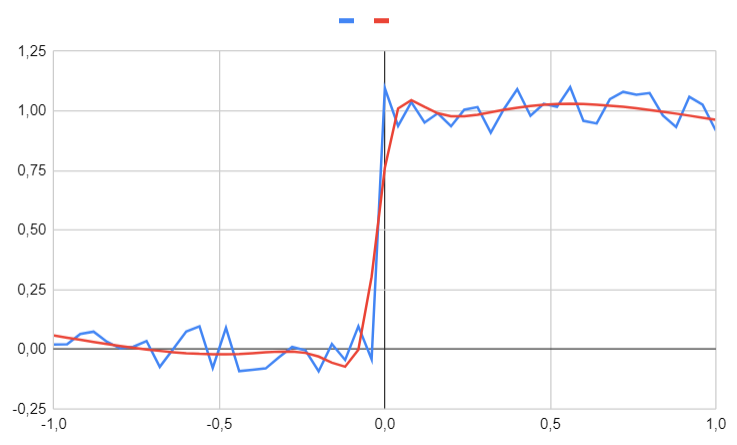
We can see that the neural network successfully identifies the underlying function. Now, let's predict an unseen value, such as $0.753$.
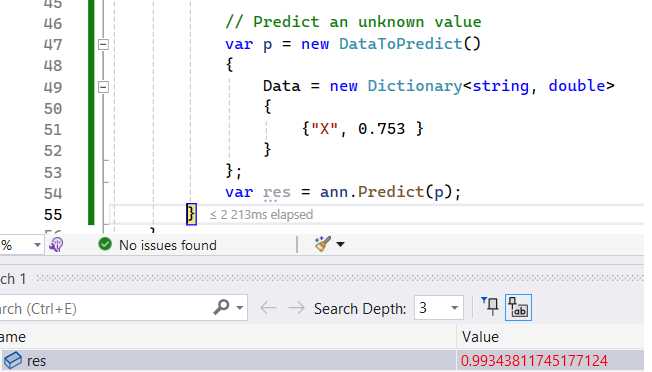
The neural network predicts $0.9934$, while the expected value is $1$.
From these various examples, we can see that neural networks are well-suited for approximating a range of functions, including some that are not even continuous. However, in the next post, we will explore the weaknesses of these data structures.
Neural networks for regression - a comprehensive overview - Part 6