Implementing a simple garbage collector in C# - Part 6
In the previous article, we acknowledged that fragmentation could pose a significant challenge with the mark-and-sweep algorithm. Here, we attempt to address this issue with the mark-and-compact algorithm.
As before, we will allocate a heap of 64 characters, and we will consider it impossible to claim additional space from the operating system.
1public MarkAndCompactGarbageCollector()
2{
3 _threads = new List<RuntimeThread>();
4 _heap = new RuntimeHeap(64);
5}
Implementing the ExecuteInstruction method
This method remains identical to what was seen in the last article.
1public override void ExecuteInstruction(Instruction instruction)
2{
3 if (instruction.Operation == "CREATE_THREAD")
4 {
5 AddThread(instruction.Name);
6 return;
7 }
8
9 var thread = _threads.FirstOrDefault(x => x.Name == instruction.Name);
10 if (thread == null) return;
11
12 if (instruction.Operation == "PUSH_ON_STACK")
13 {
14 thread.PushInstruction(instruction.Value);
15 }
16 if (instruction.Operation == "POP_FROM_STACK")
17 {
18 thread.PopInstruction();
19 }
20}
Implementing the Allocate method
If there is insufficient memory, the garbage collector attempts to reclaim memory and then retries the allocation process. If there is still not enough space, an exception is raised.
1public override int Allocate(string field)
2{
3 var r = AllocateHeap(field);
4 if (r == -1)
5 {
6 Collect();
7 r = AllocateHeap(field);
8 }
9
10 if (r == -1) throw new InsufficientMemoryException();
11
12 return r;
13}
1private int AllocateHeap(string field)
2{
3 var size = _heap.Size;
4 var cells = field.ToArray();
5 var requiredSize = cells.Length;
6
7 var begin = _currentPointerInTheHeap;
8
9 // Do not continue if there is not enough space.
10 if ((size - begin) < requiredSize) return -1;
11
12 for (var i = begin; i < begin + requiredSize; i++)
13 {
14 _heap.Cells[i].Cell = cells[i - begin];
15 }
16
17 var pointer = new RuntimeHeapPointer(begin, requiredSize);
18 _heap.Pointers.Add(pointer);
19
20 _currentPointerInTheHeap = _currentPointerInTheHeap + requiredSize;
21
22 return begin;
23}
Important: The AllocateHeap method is much simpler than in the previous algorithm because it maintains a pointer from which there is free space. Unlike before, it does not attempt to find the first area where there is enough memory. The allocation process is then facilitated and is terribly efficient.
What is the mark-and-compact algorithm ?
The mark-and-compact algorithm addresses the issue of heap fragmentation by compacting memory, ensuring that free space is contiguous.
The algorithm consists of two main phases:
- The marking phase is similar to the mark-and-sweep algorithm. It identifies and marks live objects in the heap, typically starting from root references and traversing through the object graph. Live objects are marked as reachable, while dead objects remain unmarked.
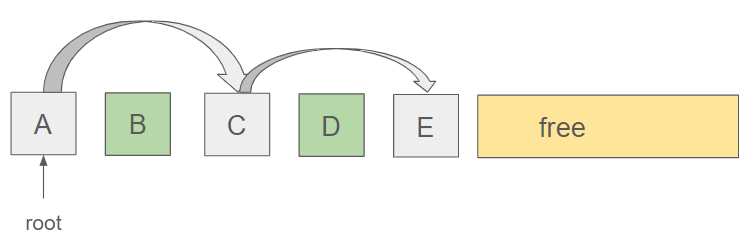
- The compacting phase follows: the algorithm rearranges the live objects in memory to eliminate fragmentation. It compacts the live objects, moving them to one end of the heap, and updates references accordingly. The compacted memory region ensures that free space becomes contiguous, mitigating the impact of external fragmentation.

The algorithm is more complex to implement compared to the mark-and-sweep algorithm and introduces additional runtime overhead, as it involves moving live objects in memory. Despite its complexity, the mark-and-compact algorithm is valuable in scenarios where efficient memory usage and reduced fragmentation are critical considerations.
1public override void Collect()
2{
3 MarkFromRoots();
4 Compact();
5}
Implementing the marking phase
The mark-and-compact algorithm must commence its traversal from roots. What constitutes these roots? Typically, they encompass global variables or references contained in the frame of each stack. In our simplified example, we will define roots as solely comprising the objects referenced in the stack.
1private void MarkFromRoots()
2{
3 var pointers = _heap.Pointers;
4 foreach (var root in _threads.SelectMany(x => x.Roots))
5 {
6 var startIndexInTheHeap = root.Value.StartIndexInTheHeap;
7
8 var pointer = pointers.FirstOrDefault(x => x.StartCellIndex == startIndexInTheHeap);
9 if (pointer == null) return;
10
11 pointer.SetMarked(true);
12 }
13}
At the conclusion of the procedure, live objects have been marked, whereas dead ones have not.
Implementing the compacting phase
The compacting phase scans through the entire heap and compacts the live data by relocating objects and updating the pointer values of all live references to objects that have moved.
1private void Compact()
2{
3 var cells = _heap.Cells;
4 var pointers = _heap.Pointers;
5 foreach (var pointer in pointers.Where(x => !x.IsMarked))
6 {
7 var address = pointer.StartCellIndex;
8 for (var i = address; i < address + pointer.AllocationSize; i++)
9 {
10 cells[i].Cell = '\0';
11 }
12 }
13
14 var list = new List<RuntimeHeapPointer>();
15 foreach (var pointer in pointers.Where(x => x.IsMarked))
16 {
17 pointer.SetMarked(false);
18 list.Add(pointer);
19 }
20
21 _heap.Pointers = pointers = list;
22
23 var offset = 0;
24 foreach (var pointer in pointers)
25 {
26 var begin = pointer.StartCellIndex;
27 if (begin == 0)
28 {
29 offset = offset + pointer.AllocationSize;
30 continue;
31 }
32
33 // Update roots in the stack
34 // This code is perfectible.
35 var thread = _threads.FirstOrDefault(x => x.Roots.Any(t => t.Key == begin));
36 var root = thread.Roots.FirstOrDefault(x => x.Key == begin);
37 root.Value.StartIndexInTheHeap = offset;
38 thread.Roots[offset] = root.Value; thread.Roots.Remove(begin);
39
40 // Update pointers in the heap
41 pointer.StartCellIndex = offset;
42 for (var i = begin; i < begin + pointer.AllocationSize; i++)
43 {
44 cells[offset + i - begin].Cell = cells[i].Cell;
45 cells[i].Cell = '\0';
46
47 }
48
49 offset = offset + pointer.AllocationSize;
50 }
51
52 _currentPointerInTheHeap = offset;
53}
The mark-and-compact algorithm introduces a trade-off between the overhead of updating live pointers and the benefit of faster allocation processes.
- Since the compacting phase ensures contiguous free space, the allocation process becomes faster. Allocating memory simply involves adjusting a pointer to the next available free space, resulting in efficient memory utilization.
- The process of compacting live objects involves updating references, which can introduce runtime overhead. During this phase, the algorithm needs to adjust pointers and references to reflect the new locations of live objects.
Running the program
Executing the program with the set of instructions that previously caused an exception in the mark-and-sweep algorithm reveals a noteworthy outcome: no exception is raised this time.

We observe, however, that certain objects persist in the heap for an extended duration (for instance, Jubilant in our example has been in the heap since the program's inception) and appear to never undergo reclamation. Nevertheless, during each collection cycle, these objects are visited to determine their liveness. This observation underscores the effectiveness of dividing the heap into partitions, allowing each partition to be managed using a distinct algorithm. Among these strategies, employing generational collectors has proven highly effective by focusing the reclamation effort on the youngest objects.