Implementing a simple garbage collector in C# - Part 5
In this article, we underscore the significance of the mark-and-sweep algorithm.
As before, we will allocate a heap of 64 characters, and we will consider it impossible to claim additional space from the operating system.
1public MarkAndSweepGarbageCollector()
2{
3 _threads = new List<RuntimeThread>();
4 _heap = new RuntimeHeap(64);
5}
Implementing the ExecuteInstruction method
This method remains identical to what was seen in the last article.
1public override void ExecuteInstruction(Instruction instruction)
2{
3 if (instruction.Operation == "CREATE_THREAD")
4 {
5 AddThread(instruction.Name);
6 return;
7 }
8
9 var thread = _threads.FirstOrDefault(x => x.Name == instruction.Name);
10 if (thread == null) return;
11
12 if (instruction.Operation == "PUSH_ON_STACK")
13 {
14 thread.PushInstruction(instruction.Value);
15 }
16 if (instruction.Operation == "POP_FROM_STACK")
17 {
18 thread.PopInstruction();
19 }
20}
Implementing the Allocate method
If there is insufficient memory, the garbage collector attempts to reclaim memory and then retries the allocation process. If there is still not enough space, an exception is raised.
1public override int Allocate(string field)
2{
3 var r = AllocateHeap(field);
4 if (r == -1)
5 {
6 Collect();
7 r = AllocateHeap(field);
8 }
9
10 if (r == -1) throw new InsufficientMemoryException();
11
12 return r;
13}
1private int AllocateHeap(string field)
2{
3 var size = _heap.Size;
4 var cells = field.ToArray();
5 var requiredSize = cells.Length;
6
7 // We need to find a contiguous space of requiredSize char.
8 var begin = 0;
9 while (begin < size)
10 {
11 var c = _heap.Cells[begin];
12 if (c.Cell != '\0')
13 {
14 begin++;
15 continue;
16 }
17
18 // Do not continue if there is not enough space.
19 if ((size - begin) < requiredSize) return -1;
20
21 // c = 0 => This cell is free.
22 var subCells = _heap.Cells.Skip(begin).Take(requiredSize).ToArray();
23 if (subCells.All(x => x.Cell == '\0'))
24 {
25 for (var i = begin; i < begin + requiredSize; i++)
26 {
27 _heap.Cells[i].Cell = cells[i - begin];
28 }
29
30 var pointer = new RuntimeHeapPointer(begin, requiredSize);
31 _heap.Pointers.Add(pointer);
32
33 return begin;
34 }
35
36 begin++;
37 }
38
39 return -1;
40}
Important: The allocation process consistently seeks contiguous free space (line 23 of the source code above). For instance, if it has to allocate 8 cells, it must locate 8 free contiguous cells. This observation will prove crucial in the subsequent sections (see below).
What is the mark-and-sweep algorithm ?
The mark-and-sweep algorithm consists of two main phases: marking and sweeping.
- In the marking phase, the algorithm traverses through all the objects in the heap, starting from the roots (typically global variables or objects directly referenced by the program). It marks each visited object as "reachable" or "live" by setting a specific flag or attribute. Objects not marked during this traversal are considered unreachable and are potentially candidates for deallocation.
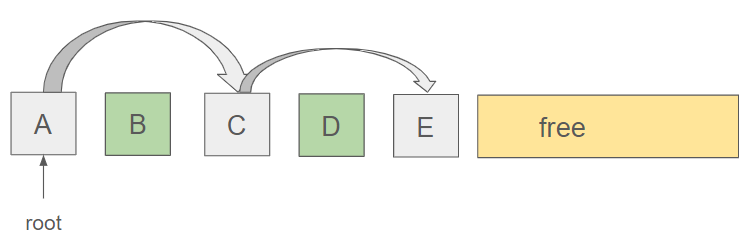
- In the sweeping phase, the algorithm scans through the entire heap, identifying and deallocating memory occupied by unmarked (unreachable) objects. The memory occupied by marked (reachable) objects is retained. After sweeping, the heap is once again considered a contiguous block of free memory, ready for new allocations.

The mark-and-sweep algorithm is known for its simplicity and effectiveness in identifying and reclaiming memory that is no longer in use. However, it has some drawbacks as we will see next.
To sum up, an object is considered dead (and therefore reclaimable) until it demonstrates otherwise by being reachable from somewhere in the program.
1public override void Collect()
2{
3 MarkFromRoots();
4 Sweep();
5}
Implementing the marking phase
The mark-and-sweep algorithm must commence its traversal from roots. What constitutes these roots? Typically, they encompass global variables or references contained in the frame of each stack. In our simplified example, we will define roots as solely comprising the objects referenced in the stack.
1private void MarkFromRoots()
2{
3 var pointers = _heap.Pointers;
4 foreach (var root in _threads.SelectMany(x => x.Roots))
5 {
6 var startIndexInTheHeap = root.Value.StartIndexInTheHeap;
7
8 var pointer = pointers.FirstOrDefault(x => x.StartCellIndex == startIndexInTheHeap);
9 if (pointer == null) return;
10
11 pointer.SetMarked(true);
12 }
13}
At the conclusion of the procedure, live objects have been marked, whereas dead ones have not.
Implementing the sweeping phase
The sweeping phase scans through the entire heap and reclaims memory from objects that are not marked.
1private void Sweep()
2{
3 var cells = _heap.Cells;
4 var pointers = _heap.Pointers;
5 foreach (var pointer in pointers.Where(x => !x.IsMarked))
6 {
7 var address = pointer.StartCellIndex;
8 for (var i = address; i < address + pointer.AllocationSize; i++)
9 {
10 cells[i].Cell = '\0';
11 }
12 }
13
14 var list = new List<RuntimeHeapPointer>();
15 foreach (var pointer in pointers.Where(x => x.IsMarked))
16 {
17 pointer.SetMarked(false);
18 list.Add(pointer);
19 }
20
21 pointers = list;
22}
In this procedure, we don't forget to reinitialize marked pointers and set them to unmarked to ensure that the next collection works again in a clean slate.
Running the program
We will execute the program with two lists of instructions. The first one is identical to the one in the previous article. The second one will highlight a phenomenon specific to this algorithm known as fragmentation.
With the same set of instructions as before, we observe that the program runs until the end with no exception raised. The word "Cascade" was correctly allocated because the garbage collector succeeded in reclaiming sufficient memory.

It becomes evident that this algorithm is superior to the previous one, ensuring that memory is correctly reclaimed when needed. However, in the example below, we will observe an undesirable effect when we slightly modify our instructions and attempt to allocate memory for a long word (16 letters).
1...
2thread1;PUSH_ON_STACK;Enigmatic
3thread2;POP_FROM_STACK;
4thread1;PUSH_ON_STACK;Cascade
5thread2;POP_FROM_STACK;
6thread2;PUSH_ON_STACK;GarbageCollector <= 16-letter words
Curiously, an exception is raised even though there appears to be enough free memory in the heap.

There are 19 free cells in the heap and we are attempting to allocate 16 cells, so why doesn't the garbage collector manage to perform the task ?
In reality, the garbage collector attempts to locate 16 free CONTIGUOUS cells, but it seems that the heap does not possess them. Although it has more than 16 free cells, these are not contiguous, rendering the allocation impossible. This phenomenon is known as fragmentation and has some undesirable effects.
More generally, heap fragmentation refers to a situation where the free memory in a heap is scattered in non-contiguous blocks, making it challenging to allocate a large, contiguous chunk of memory, even if the total free space is sufficient. While the total amount of free memory may be substantial, the scattered nature of these blocks hinders the allocation of large, contiguous portions of memory.
In the context of the mark-and-sweep algorithm, the need for contiguous memory blocks for certain allocations can be impeded by the scattered arrangement of free memory cells in the heap. As a consequence, even if the total free space is adequate, the inability to find a sufficiently large, contiguous segment can lead to allocation failures.
Addressing heap fragmentation is therefore crucial for optimizing memory usage and improving the performance of a garbage collector.